
Треугольник Паскаля
Блез Паскаль

♠ Блез Паскаль ♠
( 19 июня 1623 – 19 августа 1662 гг.)
Французский математик, физик, литератор и философ.
Классик французской литературы, один из основателей математического анализа, теории вероятностей и проективной геометрии, создатель первых образцов счётной техники, автор основного закона гидростатики
"Предмет математики настолько серьезен, что нельзя упускать случая сделать его немного занимательным"
Блез Паскаль
Свойства
• Сумма чисел n-й строки Паскаля равна 2n (потому что при переходе от каждой строки к следующей сумма членов удваивается , а для нулевой строки она равна 20=1).
• Все строки Паскаля симметричны (потому что при переходе от каждой строки к следующей свойство симметричности сохраняется).
• Каждый член строки Паскаля с номером n делится на t, когда t простое число, а n – степень этого простого числа.
• В треугольнике Паскаля через бесконечный ряд Нилаканты можно найти число Пи.
• Значение строки, если каждая запись считается десятичным знаком (имеется в виду, что числа больше 9 переносятся соответственно), является степенью 11 (11n для строки n).
• В любой строчке n, где n является четным, средним членом за вычетом члена в двух точках слева равен каталонскому числу ( n\2+1).
• Для измерения нечётных терминов в строке n необходимо преобразовать n в двоичную форму.
• Каждое число в треугольнике равно количеству способов добраться до него из вершины, перемещаясь либо вправо – вниз, либо влево – вниз.
• Все числа в n-й строке, кроме единиц, делятся на число n, если и только если n является простым числом 10.
• Если в строке с нечётным номером сложить все числа с порядковыми номерами вида 3n, 3n+1, 3n+2, то первые две суммы будут равны, а третья на 1 меньше.
• Если в треугольнике Паскаля все нечётные числа окрасить в чёрный цвет, а чётные – в белый, то образуется треугольник Серпинского.
• Четвертое число является тетраэдрическим.
• Сумма чисел восходящей диагонали, начинающейся с первого элемента ( n -1)-й строки, есть n – е число Фибоначчи.
• Первое и последние числа равны 1.
• Второе и предпоследние числа равны n.
• Каждое число треугольника Паскаля, уменьшенное на единицу, равно сумме всех чисел, заполняющих параллелограмм, ограниченный диагоналями, на пересечении которых находится этот элемент.
• Каждое число в треугольнике Паскаля равно, где — номер строки, — номер (отсчет ведется с нуля) элемента в строке.
•Числа, стоящие на горизонтальных строках треугольника Паскаля, - это биномиальные коэффициенты, то есть коэффициенты разложения n (a+b) по степеням.
• Третье число равно треугольному числу (количеству кружков, которые можно расставить в виде равностороннего треугольника, т. е. 1, 3, 6, 10): Tn-1 = n (n - 1) / 2.
• Для того чтобы его обнаружить, нужно записать элементы этой схемы в виде таблицы со сдвигом строк на 2 позиции. Затем отмечают числа, делящиеся на номер строки. Оказывается, что номер столбца, в котором выделены все числа, является простым числом.
• В каждой строке схемы сумма чисел на четных местах равна сумме элементов на нечетных местах.
• 56 гиперядер, образующих тетраэдр в пятимерном пространстве, можно уложить на гиперплоскости так, что они выстроятся в виде трехмерного тетраэдра (однако если бы мы попытались выложить из 56 ядер треугольник, то одно ядро осталось бы лишним).
•Каждое число треугольника Паскаля равно сумме предыдущей диагонали, стоящей над этим числом.
•Треугольник Паскаля позволяет объяснить принцип действия так называемой доски Гальтона — механического устройства, служащего для демонстрации приближенного гауссовского распределения
•Третья диагональ треугольника Паскаля - это «пирамидальные» числа или, более точно, тетраэдральные числа, показывающие сколько шаров может быть уложено в виде треугольной пирамиды (тетраэдра).
•Первая диагональ треугольника Паскаля – это натуральные числа, идущие по порядку











Вариации треугольника
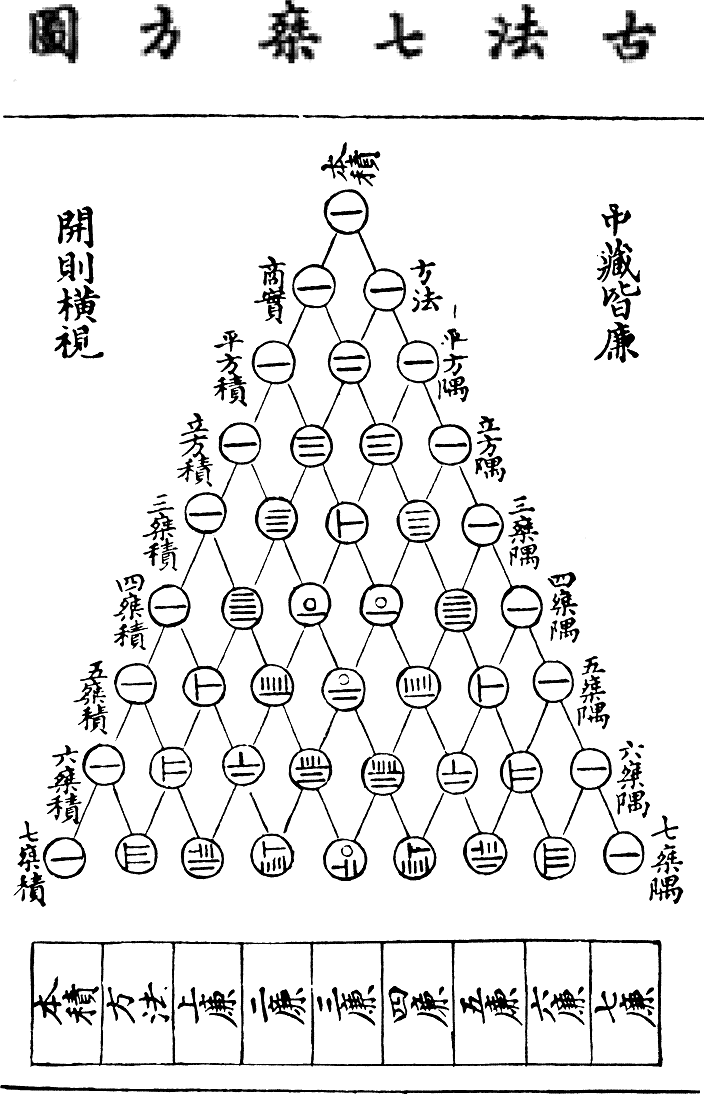
В 1303 году была выпущена книга «Яшмовое зеркало четырёх элементов» китайского математика Чжу Шицзе .
Данный треугольник отличается от треугольника Паскаля лишь манерой написания цифр , в остальном они схожи .
Треугольник Тартальи из General Trattato di Numeri et Misure , часть II, книга 2, стр. 69. Никколо Фонтана Тарталья
Главное отличие в том , что у треугольника Тартальи по краям записаны числа от 2 до 3 .

В комментарии индийского математика X века Халаюдхи к трудам другого математика, Пингалы.
Данные треугольники в сравнении с треугольником Паскаля , отличаются манерой заполнения.

Данный треугольник носит название треугольника Люка, так как суммы чисел, стоящих на восходящих диагоналях, дают последовательность чисел Люка: 1, 3, 4, 7, 11, 18, / которые могут быть определены как
Ln=Ln-1+Ln-2, L0=2, L1=1
Отличие треугольника Люка от треугольника Паскаля заключается в том, что число в новой ячейке не является суммой двух предыдущих чисел, а является суммой цифр осей. Помимо этого к треугольнику Люка нужны добавочные оси с числами от 0 до n

Из чисел (fm,n), удовлетворяющих уравнениям
fm,n=fm-1,n+fm-2,n,
fm,n=fm-1,n-1+fm-2,n-2, где с начальными условиями f0,0=f1,0=f1,1=f2,1=1 строится следующий треугольник.
fm,n =fn fn-m , m Є n Є 0, где fn - n - е число Фибоначчи. Построенный треугольник назван треугольником Фибоначчи.
В отличие от треугольника Паскаля в треугольнике Фибоначчи новое число получается из-за сложения двух предыдущих чисел в из одной диагонали. В треугольнике Паскаля складываются два числа из строки.Между рядом Фибоначчи и треугольником Паскаля существует еще одна любопытная связь. Образуем для каждой восходящей диагонали треугольника Паскаля сумму всех стоящих на этой диагонали чисел. Получим для первой диагонали 1, для второй 1, для третьей 2, для четвертой 3, для пятой 5. Мы получили не что иное, как пять начальных чисел Фибоначчи. Оказывается, что всегда сумма чисел n-й диагонали есть n-е число Фибоначчи

Это треугольник Трибоначчи. Он назван так потому, что суммы элементов, стоящих на восходящих диагоналях, образуют последовательность чисел Трибоначчи: 1,1,2,4,7,13,24,44,..., которая может быть определена следующим рекуррентным соотношением: tn+3 = tn+2 + tn+1 + tn с начальными условиями t0 = 1, t1 = 1, t2 = 2

Перед нами треугольник, составленный из одних знаков, плюсов и минусов, по принципу образования треугольника Паскаля. В отличие от последнего, он расположе�н основанием вверх. Треугольник называется "Знаковый треугольник"

Треугольник Петра Апиана
Этот треугольник воспроизведен на титульном листе учебника арифметики, написанном в начале XVI Петром Апианом, астрономом из Ингольтштадского университета.
Пожалуй главное отличие этого треугольника от треугольника Паскаля заключается в том , что значения данного треугольника крайне отличаются .К примеру , в его вершине и по бокам находятся не цифры 1

Треугольник Серпинского
Фрактал, один из двумерных аналогов множества Кантора, математическое описание которого опубликовал польский математик Вацлав Серпинский в 1915 году. Также известен как «салфетка» Серпинского.
Если в треугольнике Паскаля все нечётные числа окрасить в чёрный цвет, а чётные – в белый, то образуется треугольник Серпинского

Треугольник Омар Хайяма
Треугольник исследуется также Омаром Хайямом около 1100 года, поэтому в Иране эту схему называют треугольником Хайяма
